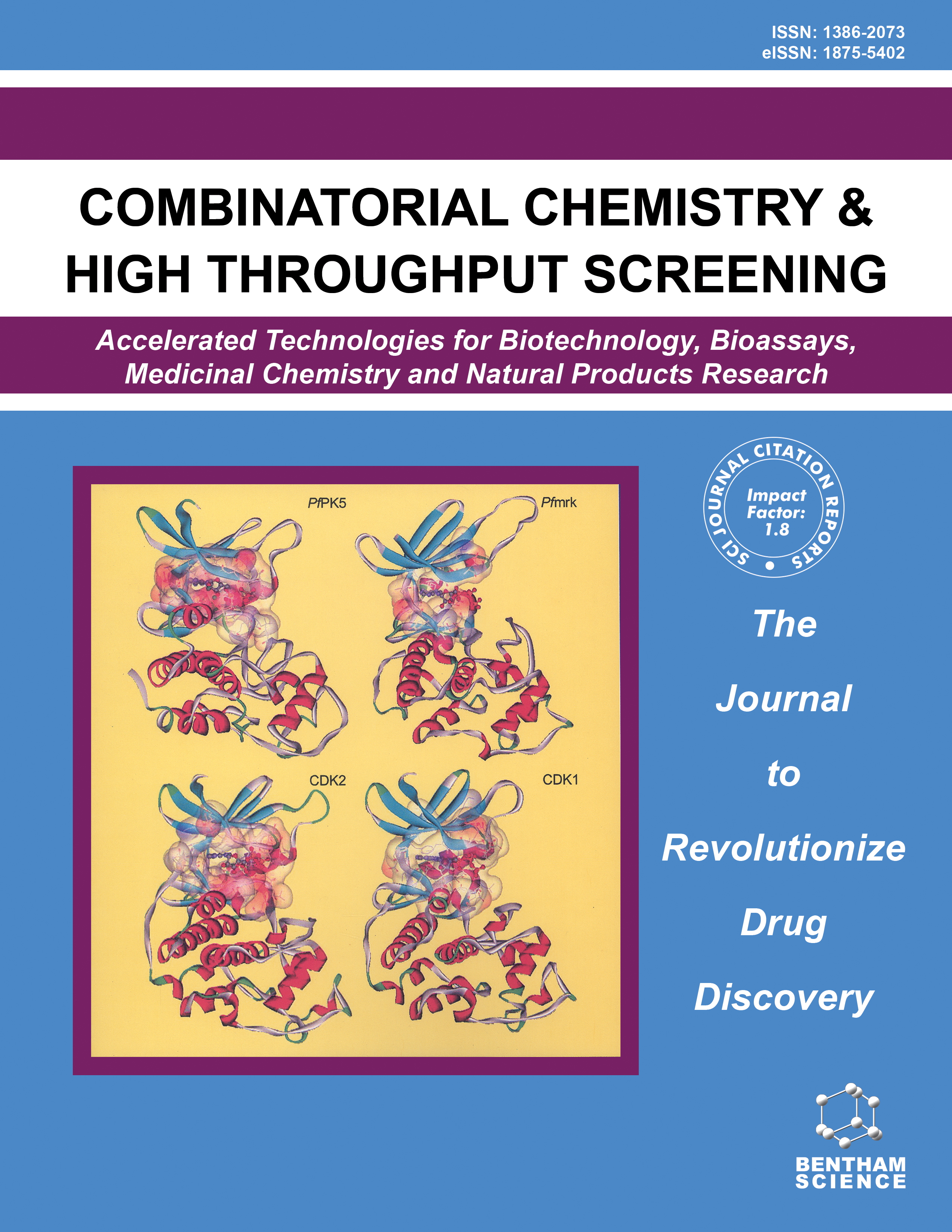
Combinatorial Chemistry & High Throughput Screening - Volume 11, Issue 9, 2008

In chemistry, there is broad use of graphs and graph-theoretical invariants derived from them. Less known are directed graphs, as e.g., motivated in reaction networks. Here, the focus is on directed graphs derived from order theory. General approaches based on the structure of molecules as well as those derived from multivariate aspects in evaluation are discussed.

The periodic law, manifested in the chart of the elements, is so fundamental in chemistry and related areas of physics that the question arises “Might periodicity among molecules also be embodied in a periodic system?” This review paper details how a particular periodic system of gas-phase diatomic molecules, allowing for the forecasting of thousands of new data, was developed. It can include ionized and even quarked-nuclei molecules and it coincides with locality (averaging) and the additivity found in some data; it has interesting vector properties, and it may be related in challenging ways to partial order. The review then explains how periodic systems for triatomic and four-atomic species are evolving along a similar path. The systems rest largely upon exhaustive comparisons of tabulated data, relate to some extent to the octet rule, and include reducible representations of the dynamic group SO(4) in higher spaces. Finally, the paper shows how periodicity can be quantified in data for larger molecules. Data for properties of homologous or substituted molecules, in any phase, are quantified with a vector index, and the index for one set can be transformed into that for another set.

Combinatorial properties of graphs and groups of physico-chemical interest are described. A type of mathematical modeling is applied which involves “translating” algebraic expressions into graphs. The idea is applied to both graph theory and group theory. The former topic includes objects of importance in physics and chemistry such as trees, polyomino graphs, king boards, etc. Our study along these lines emphasizes nonadjacency relations, graph-generation, quasicrystals, continued fractions, fractals, and general ordering schemes of graphs. The second part of the paper considers certain colored graphs as models of several group-theoretical concepts including coset representations of groups, subduction of groups, character tables, and mark tables which are essential to the understanding of recent developments of combinatorial enumeration in chemistry.

Reaction networks are viewed as derived from ordinary molecular structures related in reactant-product pairs so as to manifest a chemical super-structure. Such super-structures then are candidates for applications in a general combinatoric chemistry. Notable additional characterization of a reaction super-structure occurs when such reaction graphs are directed, as for example when there is progressive substitution (or addition) on a fixed molecular skeleton. Such a set of partially ordered entities is in mathematics termed a poset, which further manifests a number of special properties, as then might be utilized in different applications. Focus on the overall “super-structural” poset goes beyond ordinary molecular structure in attending to how a structure fits into a (reaction) network, and thereby brings an extra “dimension” to conventional stereochemical theory. The possibility that different molecular properties vary smoothly along chains of interconnections in such a super-structure is a natural assumption for a novel approach to molecular property and bioactivity correlations. Different manners to interpolate/ extrapolate on a poset network yield quantitative super-structure/activity relationships (QSSARs), with some numerical fits, e.g., for properties of polychlorinated biphenyls (PCBs) seemingly being quite reasonable. There seems to be promise for combinatoric posetic ideas.

When ranking objects (like chemicals, geographical sites, river sections, etc.) by multicriteria analysis, it is in most cases controversial and difficult to find a common scale among the criteria of concern. Therefore, ideally, one should not resort to such artificial additional constraints. The theory of partially ordered sets (or posets for short) provides a solid formal framework for the ranking of objects without assigning a common scale and/or weights to the criteria, and therefore constitutes a valuable alternative to traditional approaches. In this paper, we aim to give a comprehensive literature review on the topic. First we formalize the problem of ranking objects according to some predefined criteria. In this theoretical framework, we focus on several algorithms and illustrate them on a toy example. To conclude, a more realistic realworld application shows the power of some of the algorithms considered in this paper.

We discuss various ways in which to construct and process partial order relations or partially ordered sets (posets) in the context of ranking objects on the basis of multiple criteria. Oftentimes, it is undesirable or even impossible to devise a weighting scheme to compute a final score on the basis of the criteria. An alternative is then to restrict oneself to the information contained in the partial ordering of all objects implied by the criteria. We will consider some ways in which one can exploit partial order relations to determine a ranking of a collection of objects. More exactly, we will examine how to combine information coming from two sources, both for the case in which the sources are considered to be equally important, as well as for the case in which one source of information should take priority. We illustrate the concepts on pollution data coming from 59 regions in Baden-Wurttemberg.

Principles of partial order applied to ranking are explained. The Hasse diagram technique (HDT) is the application of partial order theory based on a data matrix. In this paper, HDT is introduced in a stepwise procedure, and some elementary theorems are exemplified. The focus is to show how the multivariate character of a data matrix is realized by HDT and in which cases one should apply other mathematical or statistical methods. Many simple examples illustrate the basic theoretical ideas. Finally, it is shown that HDT is a useful alternative for the evaluation of antifouling agents, which was originally performed by amoeba diagrams.