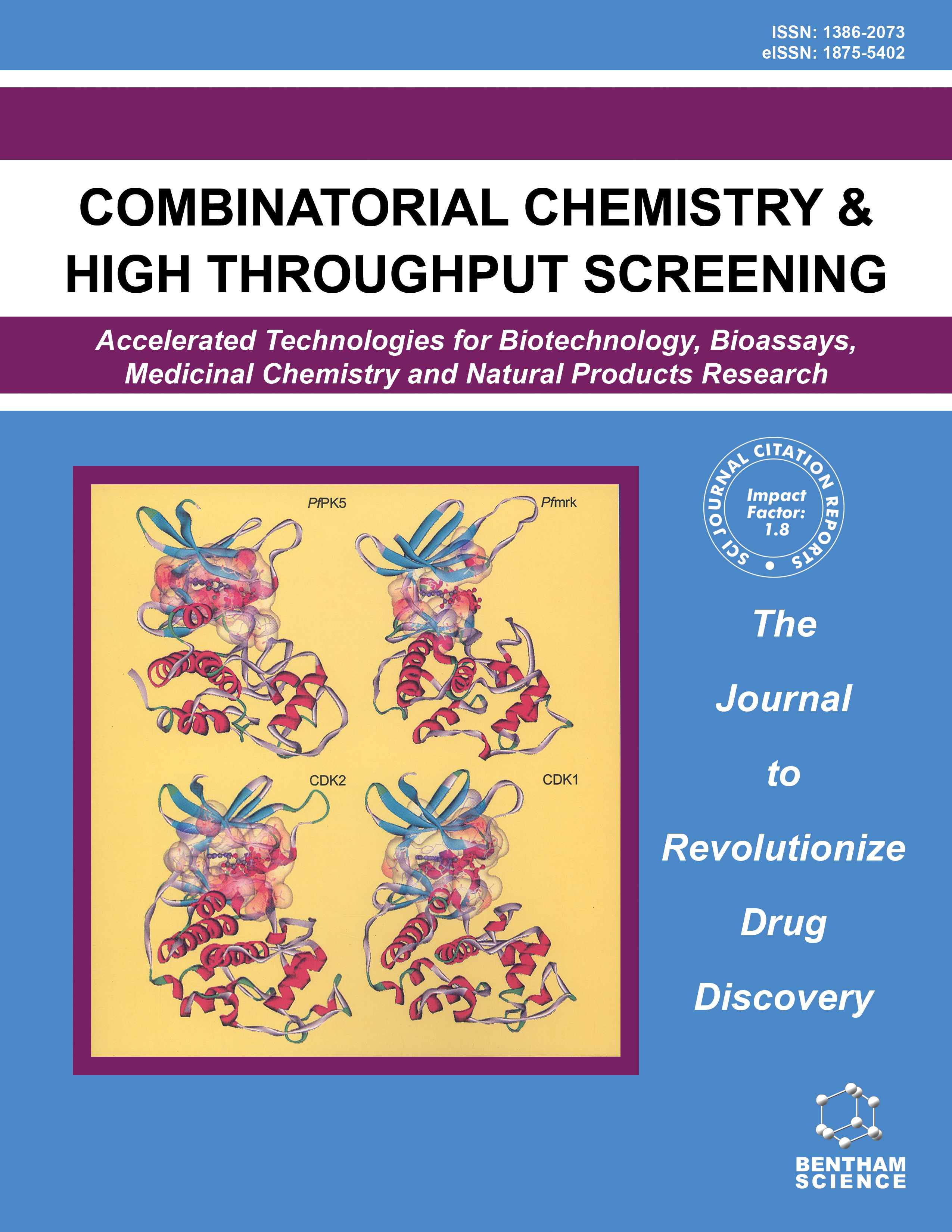
Combinatorial Chemistry & High Throughput Screening - Volume 25, Issue 3, 2022

The deluge of biological sequences ranging from those of proteins, DNA and RNA to genomes has motivated to devise models to represent them, which are further used to contrast those sequences. Here we present a brief bibliometric description of the research area devoted to the representation of biological sequences and highlight the semiotic elements of this process. Finally, we argue that this research area must learn from the evolution of mathematical chemistry and try to avoid its pitfalls.

The exponential growth in the depositories of biological sequence data has generated an urgent need to store, retrieve and analyse the data efficiently and effectively for which the standard practice of using alignment procedures are not adequate due to high demand on computing resources and time. Graphical representation of sequences has become one of the most popular alignment-free strategies to analyse the biological sequences where each basic unit of the sequences – the bases adenine, cytosine, guanine and thymine for DNA/RNA, and the 20 amino acids for proteins – are plotted on a multi-dimensional grid. The resulting curve in 2D and 3D space and the implied graph in higher dimensions provide a perception of the underlying information of the sequences through visual inspection; numerical analyses, in geometrical or matrix terms, of the plots provide a measure of comparison between sequences and thus enable study of sequence hierarchies. The new approach has also enabled studies of comparisons of DNA sequences over many thousands of bases and provided new insights into the structure of the base compositions of DNA sequences. In this article we review in brief the origins and applications of graphical representations and highlight the future perspectives in this field.

Background: Biological macromolecules, namely, DNA, RNA, and protein, have their building blocks organized in a particular sequence and the sequential arrangement encodes the evolutionary history of the organism (species). Hence, biological sequences have been used for studying evolutionary relationships among the species. This is usually carried out by Multiple Sequence Algorithms (MSA). Due to certain limitations of MSA, alignment-free sequence comparison methods were developed. The present review is on alignment-free sequence comparison methods carried out using the numerical characterization of DNA sequences. Discussion: The graphical representation of DNA sequences by chaos game representation and other 2-dimensional and 3-dimensional methods are discussed. The evolution of numerical characterization from the various graphical representations and the application of the DNA invariants thus computed in phylogenetic analysis are presented. The extension of computing molecular descriptors in chemometrics to the calculation of a new set of DNA invariants and their use in alignment-free sequence comparison in an N-dimensional space and construction of phylogenetic trees are also reviewed. Conclusion: The phylogenetic tress constructed by the alignment-free sequence comparison methods using DNA invariants were found to be better than those constructed using alignment-based tools such as PHLYIP and ClustalW. One of the graphical representation methods is now extended to study viral sequences of infectious diseases for the identification of conserved regions to design peptidebased vaccines by combining numerical characterization and graphical representation.

Aim and Objective: The similarities comparison of biological sequences is an important task in bioinformatics. The methods of the similarities comparison for biological sequences are divided into two classes: sequence alignment method and alignment-free method. The graphical representation of biological sequences is a kind of alignment-free method, which constitutes a tool for analyzing and visualizing the biological sequences. In this article, a generalized iterative map of protein sequences was suggested to analyze the similarities of biological sequences. Materials and Methods: Based on the normalized physicochemical indexes of 20 amino acids, each amino acid can be mapped into a point in 5D space. A generalized iterative function system was introduced to outline a generalized iterative map of protein sequences, which can not only reflect various physicochemical properties of amino acids but also incorporate with different compression ratios of the component of a generalized iterative map. Several properties were proved to illustrate the advantage of the generalized iterative map. The mathematical description of the generalized iterative map was suggested to compare the similarities and dissimilarities of protein sequences. Based on this method, similarities/dissimilarities were compared among ND5 protein sequences, as well as ND6 protein sequences of ten different species. Results: By correlation analysis, the ClustalW results were compared with our similarity/dissimilarity results and other graphical representation results to show the utility of our approach. The comparison results show that our approach has better correlations with ClustalW for all species than other approaches and illustrate the effectiveness of our approach. Conclusion: Two examples show that our method not only has good performances and effects in the similarity/dissimilarity analysis of protein sequences but also does not require complex computation.

Aim and Objective: Aim and Objective: Sequence analysis is one of the foundations in bioinformatics. It is widely used to find out the feature metrics hidden in the sequence. Otherwise, the graphical representation of the biologic sequence is an important tool for sequencing analysis. This study is undertaken to find out a new graphical representation of biosequences. Materials and Methods: The transition probability is used to describe amino acid combinations of protein sequences. The combinations are composed of amino acids directly adjacent to each other or separated by multiple amino acids. The transition probability graph is built up by the transition probabilities of amino acid combinations. Next, a map is defined as a representation from the transition probability graph to transition probability vector by the k-order transition probability graph. Transition entropy vectors are developed by the transition probability vector and information entropy. Finally, the proposed method is applied to two separate applications, 499 HA genes of H1N1, and 95 coronaviruses. Results: By constructing a phylogenetic tree, it was found that the results of each application are consistent with other studies. Conclusion: The graphical representation proposed in this article is a practical and correct method.

Background: Advancement in sequencing technology yields a huge number of genomes from a multitude of organisms on our planet. One of the fundamental tasks for processing and analyzing these sequences is to organize them in the existing taxonomic orders. Methods: Recently, we proposed a novel approach, GenFooT, for taxonomy classification using the concept of genomic footprint (GFP). The technique is further refined and enhanced in this work leading to improved accuracies in the task of taxonomic classification based on various benchmark datasets. GenFooT maps a genome sequence in a 2D coordinate space and extracts features from that representation. It uses two hyper-parameters, namely block size and number of fragments of genomic sequence while computing the feature. In this work, we propose an analysis of choosing values of those parameters adaptively from the sequences. The enhanced version of GenFooT is named GenFooT2. Results: We have tested GenFooT2 on ten different biological datasets of genomic sequences of various organisms belonging to different taxonomy ranks. Our experimental results indicate a 3% improved classification performance of the proposed GenFooT2 featured with a Logistic regression classifier as compared to GenFooT. We also performed the statistical test to compare the performance of GenFooT2 to the state-of-the-art methods including our previous method, GenFooT. Conclusion: The experimental results as well as the statistical test exhibit that the performance of the proposed GenFooT2 is significantly better.

Background: Coronavirus disease 2019 (COVID-19) caused by SARS-CoV-2 infection has become a worldwide pandemic and created an utmost crisis across the globe. To mitigate the crisis, the design of vaccine is the crucial solution. The frequent mutation of the virus demands generalized vaccine candidates, which would be effective for all mutated strains at present and for the strains that would evolve due to further new mutations in the virus. Objective: The objective of this study is to identify more frequently occurring mutated variants of SARS-CoV-2 and to suggest peptide vaccine candidates effective against the viral strains considered. Methods: In this study, we have identified all currently prevailing mutated strains of SARS-CoV-2 through 2D Polar plot and Quotient Radius (qR) characterization descriptor. Then, by considering the top eight mutation strains, which are significant due to their frequency of occurrence, peptide regions suitable for vaccine design have been identified with the help of a mathematical model, 2D Polygon Representation, followed by the evaluation of epitope potential, ensuring that there is no case of any autoimmune threat. Lastly, in order to verify whether this entire approach is applicable for vaccine design against any other virus in general, we have made a comparative study between the peptide vaccine candidates prescribed for the Zika virus using the current approach and a list of potential vaccine candidates for the same already established in the past. Results: We have finally suggested three generalized peptide regions which would be suitable as sustainable peptide vaccine candidates against SARS-CoV-2 irrespective of its currently prevailing strains as well any other variant of the same that may appear in the future. We also observed that during the comparative study using the case of E protein of Zika virus, the peptide regions suggested using the new approach that matches with the already established results. Conclusion: The study, therefore, illustrates an approach that would help in developing peptide vaccine against SARS-CoV-2 by suggesting those peptide regions which can be targeted irrespective of any mutated form of this virus. The consistency with which this entire approach was also able to figure out similar vaccine candidates for Zika virus with utmost accuracy proves that this protocol can be extended for peptide vaccine design against any other viruses in the future.

The aim of the studies is to show that graphical bioinformatics methods are good tools for the description of genome sequences of viruses. A new approach to the identification of unknown virus strains, is proposed. Methods: Biological sequences have been represented graphically through 2D and 3D-Dynamic Representations of DNA/RNA Sequences - theoretical methods for the graphical representation of the sequences developed by us previously. In these approaches, some ideas of the classical dynamics have been introduced to bioinformatics. The sequences are represented by sets of material points in 2D or 3D spaces. The distribution of the points in space is characteristic of the sequence. The numerical parameters (descriptors) characterizing the sequences correspond to the quantities typical of classical dynamics. Results: Some applications of the theoretical methods have been briefly reviewed. 2D-dynamic graphs representing the complete genome sequences of SARS-CoV-2 are shown. Conclusion: It is proved that the 3D-Dynamic Representation of DNA/RNA Sequences, coupled with the random forest algorithm, classifies successfully the subtypes of influenza A virus strains.

Background: Cerium oxide nanoparticles (CeO2 NPs) have gained their importance as engineered nanomaterials (ENMs) that have wide applications as catalysts in industry, which direct to their prominent occurrence in natural and engineered water systems. Cerium oxide nanoparticles (CeO2 NPs) have gained their importance as engineered nanomaterials (ENMs) that have wide applications as catalysts in industry, which direct to their prominent occurrence in natural and engineered water systems. In wastewater treatment plants, CeO2 NPs can stay colloidally stable and be unconstrained in the secondary effluents. As they entered into tertiary treatment, such as advanced oxidation processes (AOPs), it is noteworthy that how the generated reactive oxygen species will change the colloidal stability, aggregation, and the surface chemistry of CeO2 NPs. Aim and Objective: The study was aimed to analyze the chemical graph of the crystal structure of Ceria Oxide(cuprite) CeO2. Also, our main objective is to compute the Heat of Formation and Entropy using degree based topological indices. Materials and Methods: Chemical graph theory plays an important role in modeling and designing any chemical structure. The topological indices are the numerical invariants of a molecular graph and are very useful for predicting their physical properties. For calculation, we have utilized the combinatorial processing strategy, edge partition technique, vertex partition strategy, analytic procedures, graph hypothetical tools, degree counting technique and entirety of degrees of neighbor technique. Moreover, Matlab programming has been utilized for numerical computations and checks. We likewise utilized the maple for plotting these numerical outcomes. Results: We have computed Heat of Formation and Entropy using degree based topological indices. Our main results are based on some degree based topological indices, namely, the atom bond connectivity index ABC, geometric arithmetic index GA, general Randi index, Forgotten index, Augmented zagreb index and Balban index for the chemical graph of the crystal structure of cuprite CeO2[p, q, t] We also provide a detailed application of the computed results. Conclusion: We discuss these indices exhibited difference with the reported heat of formation and entropy of cuprite CeO2[p, q, t] In almost all the cases, an exponential increase of aforementioned indices is observed with the increase in the number of cells or other words size of cuprite CeO2[p, q, t] nanocrystal. On the other hand, a linear relationship of indices with respect to the number of formula units suggests a slight modification of these indices for an appropriate explanation of the physical properties of cuprite CeO2[p, q, t] nanocrystal of varying size and hence its prospective application in nanoceria engineering.

Background: Depression is a mental illness caused by the imbalance of important neurotransmitters such as serotonin (5-HT) and norepinephrine (NE). It is a serious neurological disorder that could be treated by antidepressant drugs. Objective: There are two major classes, such as TCAs and phenoxyphenylpropylamines, which have been proven to be broad-spectrum antidepressant compounds. Several attempts were made to design, synthesize and discover potent antidepressant compounds having the least toxicity and most selectivity towards serotonin and norepinephrine transporters. However, there is hardly any drug design based on quantitative structure-activity relationship (QSAR) and pharmacophore modeling attempted yet. Method: In the present study, many TCAs (dibenzoazepine) and phenoxyphenylpropylamine derivatives are taken into consideration for pharmacophore feature generation followed by pharmacophoric distant related descriptors based QSAR modeling. Furthermore, several five new congeners have been designed which are subjected to the prediction of biological activities in terms of serotonin receptor affinity utilizing validated QSAR models developed by us. Results: An important pharmacophoric feature point C, followed by the generation of a topography of the TCAs and phenoxyphenylpropylamine, has been predicted. The developed pharmacophoric feature-based QSAR can explain 64.2% of the variances of 5-HT receptor antagonism. The best training model has been statistically validated by the prediction of test set compounds. This training model has been used for the prediction of some newly designed congeneric compounds which are comparable with the existed drugs. Conclusion: The newly designed compounds may be proposed for further synthesis and biological screening as antidepressant agents.

Background: The valency of an atom in a molecular structure is the number of its neighboring atoms. A large number of valency based molecular invariants have been conceived, which correlate certain physio-chemical properties like boiling point, stability, strain energy and many more chemical compounds. Objective: Our aim is to study the valency based molecular invariants for four hexa chemical structures, namely hexagonal network, honeycomb network, oxide network and silicate sheet network. Methods: We use the technique of atom-bonds partition according to the valences of atoms to find results. Results and Conclusion: Exact values of valency-based molecular invariants, namely the Randi index, atom bond connectivity index, geometric arithmetic index, harmonic index, Zagreb indices, Zagreb polynomials, F-index and F-polynomial, are found for four hexa chemical structures.

Background: A topological index of a molecular graph is the numeric quantity which can predict certain physical and chemical properties of the corresponding molecule. Xu et al. introduced some graph transformations which increase or decrease the first and second multiplicative Zagreb indices and proposed a unified approach to characterize extremal (n, m)- graphs. Method: Graph transformations are used to find the extremal graphs, these transformations either increase or decrease the general multiplicative Zagreb indices. By applying the transformations which increase the general multiplicative Zagreb indices we find the graphs with maximal general multiplicative Zagreb indices and for minimal general Zagreb indices we use the transformations which decrease the index. Result: In this paper, we extend the Xu’s results and show that the same graph transformations increase or decrease the first and second general multiplicative Zagreb indices for . As an application, the extremal acyclic, unicyclic and bicyclic graphs are presented for general multiplicative Zagreb indices. Conclusion: By applying the transformation we investigated that in the class of acyclic, unicyclic and bicyclic graphs, which graph gives the minimum and the maximum general multiplicative Zagreb indices.

Aim and Objective: Nanostructures are objects whose sizes vary between microscopic and molecular. The most significant of these new elements are carbon nanotubes. These elements have extraordinary microelectronic properties and many other exclusive physiognomies. Recently, researchers have given attention to the mathematical properties of these materials. The aim and objective of this research article is to investigate the most important molecular descriptors namely Wiener, edge-Wiener, vertex-edge-Wiener, vertex-Szeged, edge-Szeged, edge-vertex-Szeged, total-Szeged, PI, Schultz, Gutman, Mostar, edge-Mostar, and total-Mostar indices of three-layered single-walled titania nanosheets. By computing these topological indices, material science researchers can have a better understanding of structural and physical properties of titania nanosheets, thereby synthesizing more easily new variants of titania nanosheets with more amenable physicochemical properties. Methods: The cut method turned out to be extremely handy when dealing with distance-based graph invariants which are in turn among the central concepts of chemical graph theory. In this method, we use the Djokovi-Winkler relation to find the suitable edge cuts to leave the graph into exactly two components. Based on the graph theoretical measures of the components, we obtain the desired topological indices by mathematical computations. Results: In this paper, distance-based indices for three-layered single-walled titania nanosheets were investigated and given the exact expressions for various dimensions of three-layered singlewalled titania nanosheets. These indices may be useful in synthesizing new variants of titania nanosheets and the computed topological indices play an important role in studies of Quantitative structure-activity relationship (QSAR) and Quantitative structure-property relationship (QSPR). Conclusion: In this paper, we have obtained the closed expressions of several distance-based topological indices of three-layered single-walled titania nanosheet TNS3 [m, n] molecular graph for the cases m > n and m < n. The graphical validations for the computed indices are done and we observe that the Wiener types, Schultz and Gutman indices perform in a similar way whereas PI and Mostar type indices perform in the same way.

Background: The energy E(G)of Graph G is defined as the sum of the absolute values of the eigenvalues of its adjacency matrix. In theoretical chemistry, within the Huckel molecular orbital (HMO) approximation, the energy levels of the π-electrons in molecules of conjugated hydrocarbons are related to the energy of the molecular graphs. Objective: The digraph with maximum digraph energy in a class of graphs is found. Methodology: Let Δn be the set consisting of digraphs with n vertices and each cycle having length = 2mod(4). The set of all the n-order directed hollow k-polygons in Δn based on a - polygon G is denoted by Hk(G). Results: In this research, by using the quasi-order relation over Δn and the characteristic polynomials of digraphs, we describe the directed hollow k-polygon with the maximum digraph energy in Hk(G). Conclusion: The n-order oriented hollow k-polygon with the maximum digraph energy among H_k (G) only contains a cycle. Moreover, such a cycle is the longest one produced in G.

Aims and Objective: A fullerene graph is a mathematical model of a fullerene molecule. A fullerene molecule, or simply a fullerene, is a polyhedral molecule made entirely of carbon atoms other than graphite and diamond. Chemical graph theory is a combination of chemistry and graph theory, where theoretical graph concepts are used to study the physical properties of mathematically modeled chemical compounds. Graph labeling is a vital area of graph theory that has application not only within mathematics but also in computer science, coding theory, medicine, communication networking, chemistry, among other fields. For example, in chemistry, vertex labeling is being used in the constitution of valence isomers and transition labeling to study chemical reaction networks Method: In terms of graphs, vertices represent atoms while edges stand for bonds between the atoms. By tvs (tes) we mean the least positive integer for which a graph has a vertex (edge) irregular total labeling such that no two vertices (edges) have the same weights. A (3,6)-fullerene graph is a non-classical fullerene whose faces are triangles and hexagons Results: Here, we study the total vertex (edge) irregularity strength of an arbitrary disjoint union of (3,6)-fullerene graphs and provide their exact values. Conclusion: The lower bound for tvs (tes) depends on the number of vertices. Minimum and maximum degree of a graph exist in literature, while to get different weights, one can use sufficiently large numbers, but it is of no interest. Here, by proving that the lower bound is the upper bound, we close the case for (3,6)-fullerene graphs.

Aim and Objective: Metal-organic network (MON) is a special class of molecular compounds comprising groups of metal ions and carbon-based ligand. These chemical compounds are examined employing one, two- or three-dimensional formation of porous ore and subfamilies of polymers. Metal-organic networks are frequently utilized in catalysis for the parting & distilling of different gases and by means of conducting solid or super-capacitor. In various scenarios, the compounds are observed to maintain a balance in the procedure of deletion or diluter of the molecule and can be rebuilt with another molecular compound. The physical solidity and mechanical characteristics of the metal-organic network have attained great attention due to the above-mentioned properties. This study was undertaken to find the polynomials of MON. Methods: Topological descriptor is a numerical number that is utilized to predict the natural correlation amongst the Physico-chemical properties of the molecular structures in their elementary networks Results: After partitioning the vertices based on their degrees, we calculate different degree-based topological polynomials for two distinct metal-organic networks with an escalating number of layers containing both metals and carbon-based ligand vertices. Conclusion: In the analysis of the metal-organic network, topological descriptors and their polynomials play an important part in modern chemistry. An analysis between the various calculated forms of the polynomials and topological descriptors through the numeric values and their graphs are also presented

Background: With the advent of the second-generation sequencing technology, the discovery of sequence alignment and sequence variation is a long-standing challenge Methods: A method based on general alignment software, SNP, and Indel software tools was proposed in this paper. By comparing the advantages of traditional alignment software, we can produce the best alignment. Results: SNP and Indel detection tools fusion research found that different depth of sequencing effect is different. When the sequence depth reaches a certain value, one of the softwares is selected for testing Conclusion: Finally, the experimental verification shows that SNP and Indel have certain advantages in comparing the effects of the fusion method.

Background: A topological index is a real number associated with a graph that provides information about its physical and chemical properties and their correlations. Topological indices are being used successfully in Chemistry, Computer Science, and many other fields. Methods: In this article, we apply the well-known Cartesian product on F-sums of connected and finite graphs. We formulate sharp limits for some famous degree-dependent indices. Results: Zagreb indices for the graph operations T(G), Q(G), S(G), R(G), and their F-sums have been computed. By using orders and sizes of component graphs, we derive bounds for Zagreb indices, F-index, and Narumi-Katayana index. Conclusion: The formulation of expressions for the complicated products on F-sums, in terms of simple parameters like maximum and minimum degrees of basic graphs, reduces the computational complexities.